Project Overview
This project involved the design, implementation, and training of an Artificial Intelligence (AI) agent to autonomously navigate a “Flappy Bird”-style canoe game. The core objective was to enable the AI to successfully pass through a series of gates by making intelligent up/down movement decisions. The primary machine learning technique employed was Logistic Regression, trained through Supervised Learning based on data simulating optimal gameplay. The AI successfully navigated 426 gates, demonstrating the effectiveness of the approach.
I. Theoretical Foundation: Logistic Regression
The AI’s decision-making process is a binary classification problem (move up/down). Logistic Regression was chosen for its ability to predict probabilities for these outcomes.
Linear Combination (z)
The model first calculates a linear combination of input features (related to the game state):
z = Ax + By + C
Where A, B, and C are coefficients learned by the model. The line where z=0 forms the decision boundary.
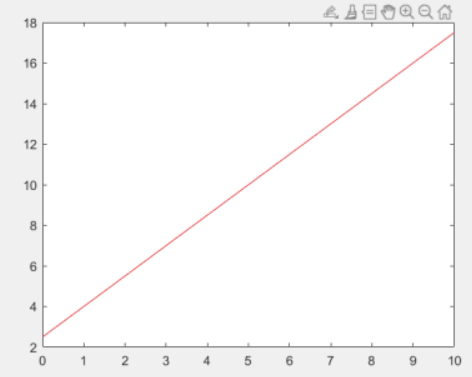
Illustrative 2D decision boundary (e.g., y = (3/2)x + 5/2) where the linear combination z equals zero, separating the input space.
Sigmoid Function (Probability Mapping)
The z value is passed through a sigmoid (logistic) function:
f(x,y) = 1 / (1 + e^-z)
This squashes z into a probability between 0 and 1.
- If
z=0, sigmoid output is0.5. - If
z > 0, output is> 0.5. - If
z < 0, output is< 0.5.
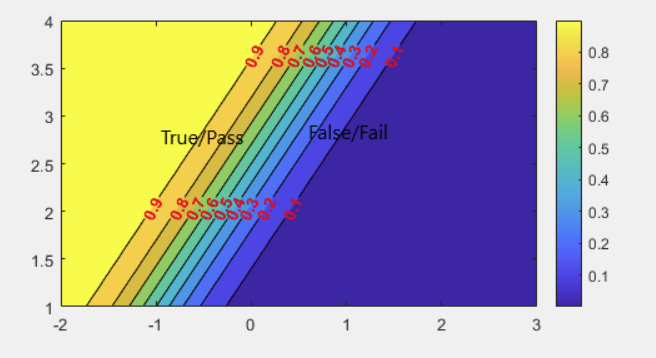
Contour plot visualizing the sigmoid function’s output. Colors represent probability, showing the transition from one class to another.
Classification
The AI uses this probability to decide its action. For instance, if the probability of needing to move up is > 0.5, the AI moves up.
II. Model Training: Learning Optimal Coefficients
Optimal values for A, B, and C were found using supervised learning:
Data Collection
Gameplay data (mydata.mat, MECH3610_Classification_Data(2).csv) was used, containing input features (game state) and target outputs (desired actions).
Cost/Loss Function
To measure model performance, two cost functions were explored:
- Sum of Squared Errors (SSE):
SSE = sum((f - Ffit)^2) - Binary Cross-Entropy Loss:
Loss = -1/M * sum(f*log(ypred) + (1-f)*log(1-ypred))(Generally preferred for classification)
Optimization with fminunc
MATLAB’s fminunc function iteratively adjusted A, B, and C to minimize the chosen cost function.
Table: Initial manual exploration of coefficients and their Sum of Squared Errors (SSE), highlighting the search for better parameters before automated optimization.
| A | B | C | SSE |
|---|---|---|---|
| 100 | 200 | 400 | 104 |
| -10 | 2 | 10 | 96 |
| -6 | 5 | 12 | 96 |
| -4 | 10 | 20 | 9.59 |
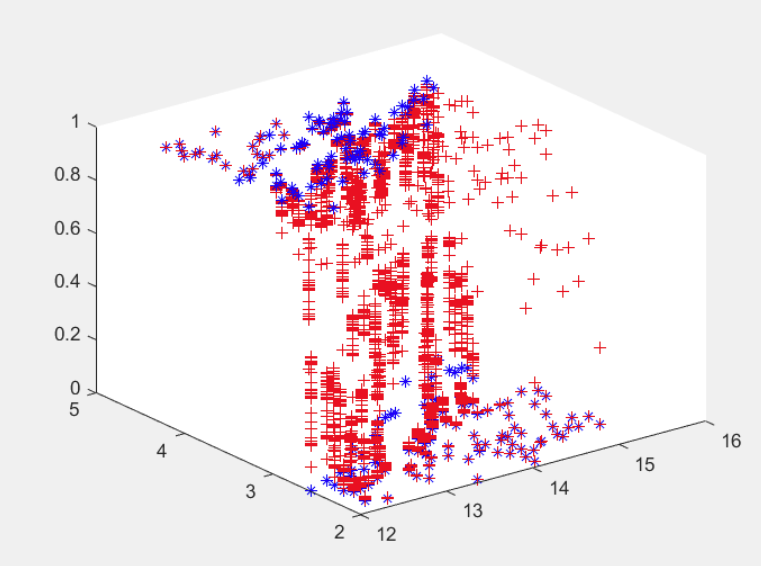
3D visualization comparing original data points (blue stars) with predictions from the optimized logistic regression model (red crosses). This illustrates how well the model learned to fit the data after optimization.
MATLAB Code Snippet: SSE Calculation
function [SSE] = sygmoidLogisticSSE(Coeefs, x, y, f)
% Assign coefficients
A = Coeefs(1);
B = Coeefs(2);
C = Coeefs(3);
% Calculate fitted values using the sigmoid function
Ffit = (1./(1+exp(-1*(A*x+B*y+C))));
% Calculate error
error = f - Ffit;
% Calculate Sum of Squared Errors
SSE = sum(error.^2);
end
MATLAB code used to calculate the Sum of Squared Errors (SSE), which was minimized by fminunc to find optimal model coefficients.
Optimal Coefficients
Optimization yielded coefficients like:
A=-4, B=10, C=20(from SSE on one dataset)A=-10.2831, B=10.7354, C=-0.4741(from cross-entropy onmydata.mat)
III. AI Implementation and Gameplay
The trained model powered the AI in the game:
Prediction Function (getPred)
The getPred(X, P) function used the learned parameters P (A, B, C) and current game state X to predict the next move via the sigmoid output.
function y_pred = getPred(X, P)
% P(1)=A, P(2)=B, P(3)=C
% X(1)=x_feature, X(2)=y_feature (simplified)
Z1 = P(1)*X(1) + P(2)*X(2) + P(3);
y_pred = 1/(1+exp(-Z1));
end
The getPred MATLAB function, forming the AI’s decision-making core by using learned parameters and game state to predict actions.
AI Behavior and Performance
The AI, using parameters from mydata.mat (likely via cross-entropy minimization), navigated by attempting to center itself in gates. This strategy led to 426 successful gate passes.
(The gameplay image at the top of the article showcases this performance.)
IV. Ethical Considerations
This project also prompted reflections on AI ethics, including data privacy, accountability, and decision-making in critical scenarios, relevant even in developing AI for more complex systems like autonomous vehicles.
V. Conclusion and Skills Demonstrated
This project successfully applied logistic regression and supervised learning to train an AI for game navigation.
Key Skills:
- Machine Learning: Logistic Regression, Supervised Learning.
- Optimization: Using MATLAB for parameter tuning.
- Programming: MATLAB for algorithm implementation, data processing, and visualization.
- AI Development: Designing and testing an AI agent.
- Data Analysis: Visualization and interpretation.
- Ethics: Ethical implications of AI.
